RC11. Building an Adder, Part 2

Daily dispatches from my 12 weeks at the Recurse Center in Summer 2023

Today we’re going to bring our adder across the finish line.

Last time we derived a full adder that required six gates in the end:

• 2 XOR gates
• 2 OR gates
• 2 AND gates

As I demo’ed in another post, each of these gates can be derived from NAND gates exclusively.

• An OR gate can be built from 3 NAND gates,
• an AND from 2,
• and an XOR – by far the most expensive of all – from 9 NAND gates, which can easily be reduced to 5.

That means our full adder would need 20 NAND gates. But after drawing it out, I noticed a few opportunities for savings and eventually got it down to 15 NANDs. Maybe it can be simplified further, I’m not sure.

Anyway. 15 NAND gates, then. But that’s just for adding two bits and a carry bit. Fun fact: If we want to add two 16-bit integers, we’d need 240 NAND gates!

Well, we’re not insane, so we’re going to make do with the Full Adder abstraction, of which we need one for each bit – i.e., 16 are needed for adding 16-bit integers. Even that’s a lot, though, so here’s how it’d all look for a 4-bit adder:

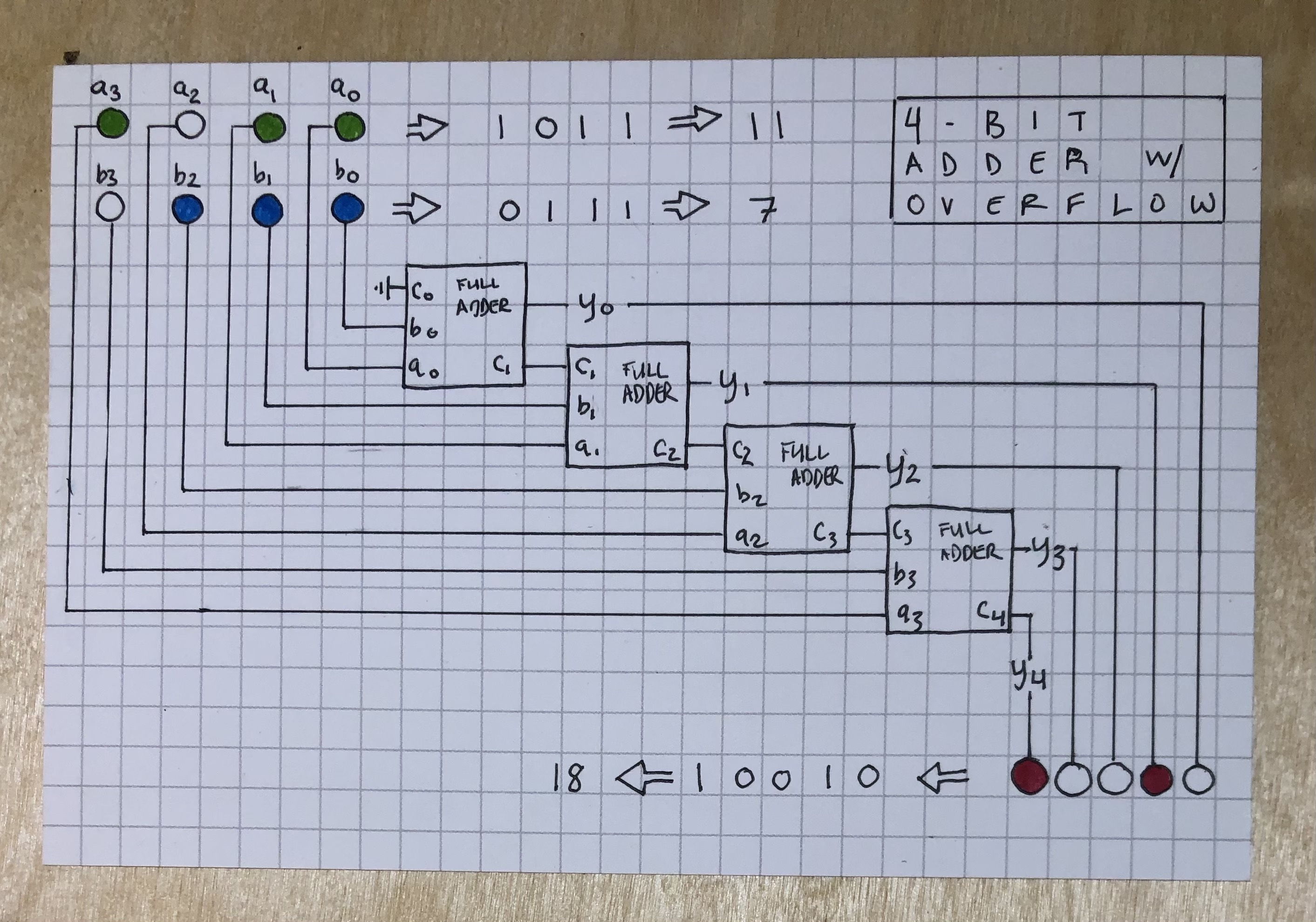
What’s happening here is that the Least Significant Bits (the bits in the 1’s place, or bits \(a_0\) and \(b_0\)) get passed into the a and b inputs of the first adder. Because there’s no carry bit for the first adder, we can pull \(c_0\) to ground. This first adder has the two outputs we expect: our least signficant sum bit \(y_0\) and carry bit \(c_1\), which belongs with the next most significant bit in the 2’s place.

Speaking of: Next we indeed move on to the next most significant bits – the bits in the 2’s place, or bits \(a_1\) and \(b_1\), which we pass to the a and b inputs of the second adder along with the \(c_1\) carry bit output from the first adder. This second adder spits out a sum bit for the 2’s place, \(y_1\) and a carry bit for the 4’s place, \(c_2\).

On and on we go. The input bits from the 4’s place, \(a_2\) and \(b_2\), go to adder number 3, which give us sum bit \(y_2\) and carry bit \(c_3\), then then the input bits from the 8’s place, \(a_3\) and \(b_3\), go to adder number 4, which gives us sum bit \(y_3\) and carry bit \(c_4\), which actually becomes our overflow sum bit \(y_4\) since there’s no more adders left.

If we want to add 8-bit integers or 16-bit integers, well, we just need more adders chained along! But that’s the main idea.

Other things that happened today

• Did some pairing on a string problem from CTCI
• Had a few good coffee chats, including with a recurser about their workflow with Obsidian (a markdown knowledge manager) and Anki (a flashcard software). Very impressed but not sure I have the discipline for Anki. However, I was very curious about Obsidian, since I’ve been keen to move away from DevonThink, which suited me during the days of dissertation research but not feels a little heavy-weight and opaque. Still, I’m not sure that moving to Obsidian is the answer right now, as attractive as writing in markdown is. So, kicking that can down the road.
• Did a linked list cycle detection problem in the Neetcode group
• Paired with a fellow nand2tetris groupie where we hammed out an ALU, which will be the subject of my next blog post. It was genuinely a surprise when our ALU suddenly worked, really a fun and productive collaborative effort.